Kreipiamųjų sistemų optimalių asimetrijų statistinė analizė.

V. Šaras, J. Kryštul; AB „Vilniaus Vingis“

Nesuvestis ir asimetrijos, vartotojo ir gamintojo charakteristikos

Su vartotojais yra derinamos kreipiamųjų sistemų (toliau KS) nesuvesties specifikacijos normos. Tai maksimaliai leistini atstumai tarp bet kokios spalvos spindulių pėdsakų kineskopo ekrane. KS gamintojams aktuali yra ne nesuvestis, o nesuvesties asimetrijos (toliau asimetrijos), kurių pagalba yra derinamas technologinis procesas. Dėl to svarbus yra šių skirtingų charakteristikų sąryšis ir suprantamos pastangos išanalizuoti jas.

Astigmatizmo, komos ir distorsijos (skleistinės geometrijos) asimetrijų specifika.

Asimetrijos parametrų erdvė yra labai didelė ir dėl to tikslinga grupuoti (ar skirstyti sluoksniais) pagal įvairius požymius. Šiuos požymius galima įvardinti sekančiai:

· Pagal elektromagnetinių linzių požymius:

o distorsijos (skleistinės geometrijos) (dvipolė linzė),

o astigmatizmo (keturpolė linzė),

o komos (šešiapolė linzė);

· Pagal vietą kineskopo ekrane:

o asimetrijas ant ašių,

o kampuose horizontalia ir vertikalia kryptimis (x, y),

o kampuose radialia ir diagonalia kryptimis (r, d),

o anizotropijos,

o specialias asimetrijas;

· Pagal asimetrijos kryptį:

o centrinę (M efekto),

o sukamąją (D efekto),

o vertikalią (N efekto),

o horizontalią (W efekto);

· Pagal sąryšį su KS ritelėmis:

o eilučių ritelėmis,

o kadrų ritelėmis;

· kt.

Jei pasižiūrėti į astigmatizmo, komos ir dalinai distorsijos asimetrijas, galima pastebėti, kad jų sandara ir skaičiavimo algoritmai analogiški, tik yra išsidėstę skirtingose vietose ir formuojami skirtingais kineskopo spinduliais. Tokiu būdu galima supaprastinti jų nagrinėjimą analizuojant vieną grupę, o išvadas pritaikyti kitiems grupės nariams. Asimetrijas ir jų žyminius tikslinga išdėstyti asimetrijų lentelėje pieš. 1, kurios pagalba daug lengviau susigaudyti šioje erdvėje.

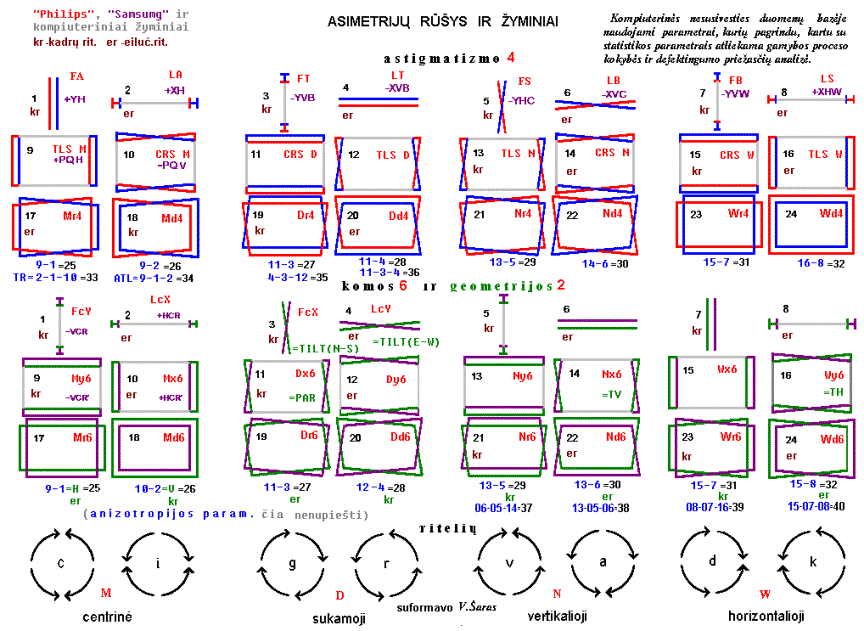
Pieš. 1. Asimetrijos parametrų lentelė

KS gamyboje renkamų duomenų specifika. Technologinio proceso charakteristikų švarumas ir šuntų įtaka.

KS gamyboje yra taikomi kelių lygių matavimai su grįžtamuoju ryšiu pieš 2. Tai

· ritelių ir impedansų matavimas,

· kontroliniai surinkimai,

· galutinė kontrolė.

Visais atvejais yra registruojamos ir analizuojamos asimetrijos bei jų ryšiai su gamybiniais objektais, kur tos asimetrijos atsiranda. Ieškomos ir šalinamos jų atsiradimo priežastys. Tokiu būdu labai svarbu, kad registruojama informacija turėtų savyje šių objektų žyminius ir dar geriau, kad turėtų šių objektų parametrus. Masinėje gamyboje dažniausiai stengiamasi turėti minimaliai būtiną jų kiekį, nes papildomi matavimai ir jų registravimas didina darbo imlumą ir savikainą, o laisvos rinkos sąlygos ir investuotojų lūkesčiai reikalauja mažinti ją. Išeitis – statistinė analizė, kompiuterizavimas, automatizavimas ir gamybinių išlaidų minimizavimas.

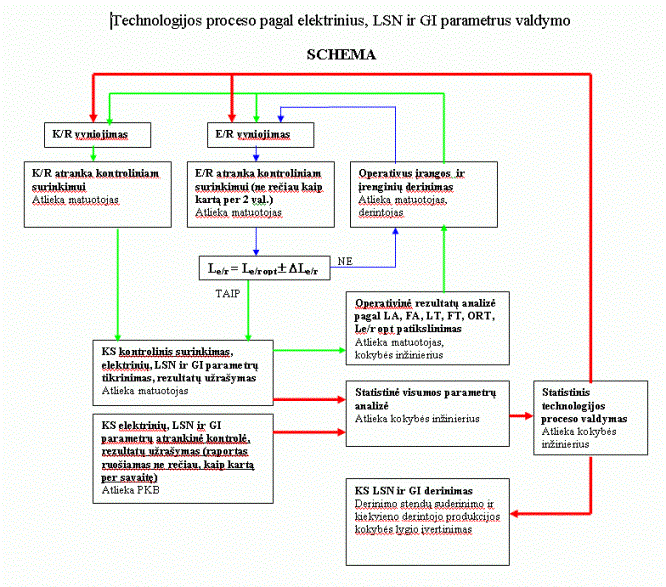
Pieš. 2. KS technologinio proceso grįžtamieji ryšiai.

KS gamyboje pagrindiniai nesuvesties matavimai yra kompiuterizuoti ir automatizuoti. Tačiau gamybinių objektų ir tiekiamų žaliavų parametrai dar nepakankamai. Dėl to tikslinga į juos atkreipti dėmesį: kompiuterizuoti šių duomenų surinkimą, išanalizuoti ryšius, sukurti ar pritaikyti atitinkamas metodikas. Pagal šių idėjų realizacijos lengvumą galima išvardinti sekančias kryptis:

· automatizuotas šuntų vietos ir dydžio registravimas, kad galima būtų tobulinti šuntų panaudojimo technologiją;

· staklių reguliavimo parametrų kompiuterizuotas registravimas, kad galima būtų efektyviau reguliuoti stakles ir kt. gamybinius objektus;

· panaudojamo laido parametrų kompiuterizuotas registravimas, kad vyniojimo procesas būtų iš anksto derinamas.

Iš visų čia paminėtų renkamų parametrų rūšių vertingiausi yra kontrolinių surinkimų duomenys. Jų pagalba galima skaičiuoti nukrypimus ir valdyti technologinį procesą, kadangi sekantys matavimai atliekami jau po magnetinių šuntų klijavimo, kurie skirti eliminuoti gamybinio proceso nukrypimus. Dėl to kontrolinių surinkimų duomenų statistikai ir analizei tenka skirti daugiausia dėmesio.

Asimetrijų koreliacinė analizė.Ritelių asimetrijų sluoksniai efektų sluoksniuose.

Aukščiau minėta, kad asimetrijos gali būti įvairiai grupuojamos. Grupes galima pavadinti sluoksniais. Tie sluoksniai gali būti lygiagretūs, gali ir susikirsti. Panagrinėsime KS ritelėms skirtą sluoksnį ir su kuriom kitų sluoksnių asimetrijom jis susikerta.

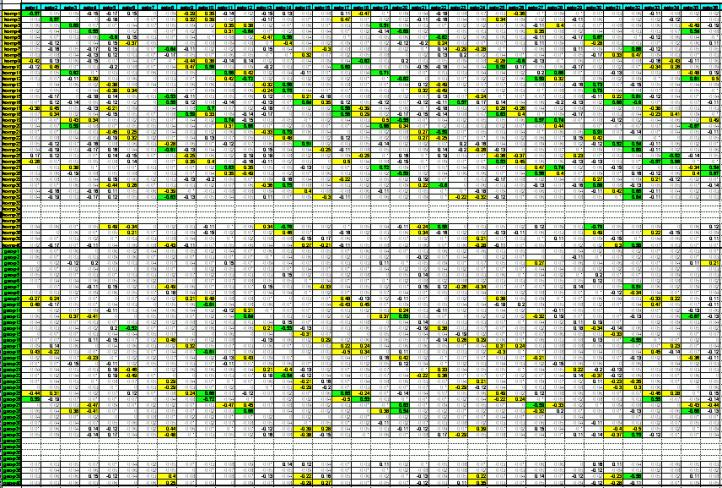
Pieš. 3. Koreliacinėje matricoje išryškėjantys asimetrijų sluoksniai

KS gamyboje labai svarbi yra ritelių vyniojimo proceso analizė, tobulinimo galimybės ir optimalūs parametrai. Dėl to buvo atlikta matavimo duomenų asimetrijų koreliacinė analizė keliems gaminiams. Visų metų matavimų didelės apimties duomenų masyvai (nuo 6000 iki 200000 KS) leido patikimai įsitikinti, kad asimetrijos parametrus galima suskirstyti į nesusikertančius eilučių ir kadrų ritelių asimetrijų sluoksnius, kuriuose yra sluoksniai, skirti asimetrijų kryptims arba efektams. Ir kiekvienas iš jų turi tik po vieną asimetriją ant ašių ir kampuose astigmatizmo, komos ir distorsijos sluoksniuose. Tai leidžia šiuos asimetrijų sluoksnius nagrinėti atskirai, nesiejant su kitais sluoksniais ir supaprastinti jų nagrinėjimo algoritmą bei gauti greitus analizės rezultatus: nustatyti konstruktyvines paklaidas arba nominalias asimetrijas arba optimumus.

Nesuvestis, asimetrijų suma ir jų normos. Koreliacinė analizė ir bandymas su atsitiktiniais rinkiniais

Kaip minėta aukščiau, su vartotojais pagrinde yra derinamos nesuvesties normos. Dėl to svarbu yra teisingai nustatyti gamybiniame procese naudojamų asimetrijų normas. Remiantis asimetrijų ir nesuvesties skaičiavimo algoritmais galima teigti, kad kiekviena asimetrija kampuose susideda iš keturių nesuvesčių kampuose, o kiekviena nesuvestis bet kuriame iš kampų susideda iš keturių asimetrijų (M, D, N ir W ef.). Kiekvienai iš M, D, N ir W efektų asimetrijų galima paskaičiuoti defektingumo tikimybes bei bendrą defektingumą. Taip pat ir kiekvienam nesuvesties kampui galima paskaičiuoti tą patį. Įvertinant tai, kad šie parametrai pasiskirstę pagal normalinį dėsnį, skaičiavimai nesunkiai realizuojami. Tokiu būdu buvo suformuota kompiuterinė programa, perskaičiuojanti parametrus ir tinkamumus bei defektingumus iš nesuvesties į asimetrijas arba atvirkščiai, remiantis tų parametrų vidurkiais, išsibarstymais, tikslo dydžiais ir pasirinktomis normomis. Normų ir parametrų grafinis vaizdas leido akivaizdžiai ir įtikimai gauti analizės rezultatus. Jos pagalba galima nagrinėti įvairius nesuvesties ir asimetrijų ryšio aspektus.

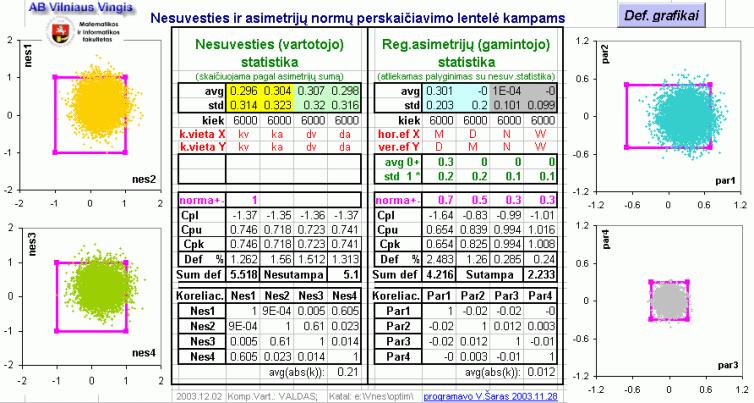
Pieš. 4. Nesuvesties ir asimetrijų normų įtakos perskaičiavimo programos forma

Vienas iš jų pavyzdžiui – kaip nepriklausomų asimetrijų išsibarstymai įtakoja į nesuvesties parametrų tarpusavio koreliacijas. Pasirodo, kad nesuvesties koreliacijos priklauso tik nuo asimetrijų išsibarstymo skirtumo. Kuo didesnis skirtumas, tuo didesnė nesuvesties koreliacija. Arba labai įdomi asimetrijų vidurkio įtaka į nesuvesties vidurkius. Visi keturi asimetrijų krypčių (efektų) tipai iššaukia didelę nesuvestį tik viename kampe. O viena asimetrija vienodai pasiskirsto visuose keturiuose nesuvesties kampuose. Žemiau pateikta lentelė parodo įvairius variantus kai asimetrijų dydis lygus 0,5.

Asimetrijų skaičius	Nesuvesties dydis	Nesuvesties kampų skaičius
1 x 0,5	0,5	4
2 x 0,5	1,0 0,0	2 2
3 x 0,5	1,5 0,5	1 3
4 x 0,5	2,0 0,0	1 3

1 lentelė. Asimetrijų skaičiaus įtaka į nesuvesties kampų skaičių ir dydį.

Esant nesuvesties pasiskirstymui (kairėje programos formos pusėje), paslinktam kuria nors įžambinės kryptimi, ją galima koreguoti atitinkama asimetrijos parametro vidurkio korekcija, kaip nurodyta sekančioje lentelėje:

Par1

Par2

Par3

Par4

Nes 1

Nes 2

Nes3

Nes4

2 lentelė. Asimetrijų vidurkio (Par) įtaka į nesuvesties (Nes) išsibarstymo kryptį.

Nesuvesties ir asimetrijų leistinų ribų (specifikacijos normų) sąryšis ir išvados

Nesuvesties ir asimetrijų leistinų ribų (specifikacijos normų) realizacijos variantų gali būti labai daug. Turint kompiuterinę programą kiekvienu atveju galima paskaičiuoti normas, kurioms esant tinkamumas ir defektingumas vienodi, optimizuoti pagal sutapimo arba nesutapimo dydį, įvertinti asimetrijų ir nesuvesties defektingumo riziką.

Keletas normų variantų nesuvesčiai kampuose pateikta žemiau esančioje lentelėje:

Asimetrijoms kampuose									nesuvesčiai kampuose
avg				std				norma	norma
Par1	Par2	Par3	Par4	Par1	Par2	Par3	Par4	Par1 2 3 4	Nes1 2 3 4
0,3	0,0	0,2	0,0	0,3	0,2	0,1	0,001	0,603	1,000
0,3	0,2	0,2	0,1	0,3	0,2	0,1	0,001	0,496	1,000
0,3	0,0	0,2	0,0	0,3	0,2	0,1	0,1	0,578	1,000
0,3	0,2	0,2	0,1	0,3	0,2	0,1	0,1	0,489	1,000
0,3	0,0	0,2	0,0	0,3	0,2	0,1	0,1	0,676;0,338	1,000

3 lentelė. Vienodo defektingumo nesuvesties ir asimetrijų normos kampuose

Šioje lentelėje tose vietose, kur nurodytos dvi asimetrijų normų reikšmės, mažesnės normos taikomos dvejoms asimetrijoms, kurių statistika su didesniu tinkamumu. Matome, kad galime manipuliuoti asimetrijų normom nekeisdami nesuvesties tinkamumą. Tokiu būdu galima įvesti realius asimetrijų statistikos duomenis, pasirinkti normas su pigesniu koregavimo šuntais keliu ir sumažinti gamybos nuostolius.

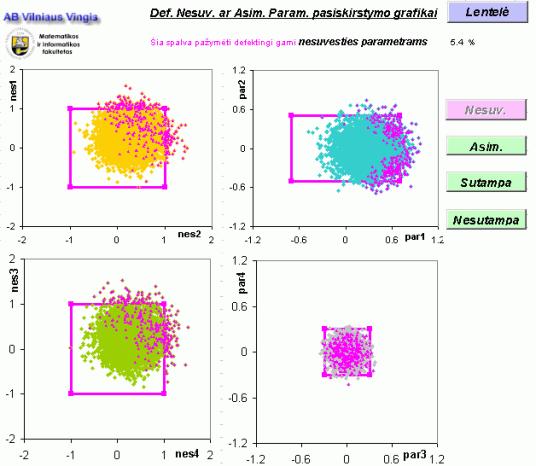
Pieš. 5. Defektingų gaminių pasiskirstymo programos forma

Žemiau normų lentelė asimetrijoms ir nesuvesčiai ant ašių:

Asimetrijoms ant ašių					nesuvesčiai ant ašių
avg		std		norma	norma
0,3	0,0	0,3	0,2	0,356	0,500
0,3	0,2	0,3	0,2	0,347	0,500
0,2	0,0	0,2	0,1	0,413	0,500
0,2	0,2	0,2	0,1	0,329	0,500
0,2	0,0	0,2	0,1	0,436;0,218	0,500
0,2	0,0	0,2	0,1	0,510;0,170	0,500

4 lentelė. Vienodo defektingumo nesuvesties ir asimetrijų normos ant ašių

Normos ant ašių mažiau skiriasi, kadangi mažiau parametrų.

G. Popovo straipsnyje „KS gaminių kokybės kontrolės įvertinimas, naudojant statistinį metodą“ (9 AB „Ekranas“ M.T. konferencijos medžiaga) yra duotas supaprastintas normų skaičiavimo algoritmas, panaudojant vidutinį kvadratinį metodą ir vienodas įvairių asimetrijų normas. Vienok tame pačiame straipsnyje parodyta, kad asimetrijų normas reikia paskirstyti atsižvelgiant į tų asimetrijų išsibarstymus ir duotas pavyzdys. Aukščiau minėta kompiuterinė normų perskaičiavimo programa akivaizdžiai parodo, kad to maža. Reikia įvertinti pilnai visą normalųjį dėsnį, ne tik su išsibarstymu, bet ir su vidurkiu. Ir konstruktyvines paklaidas reikia priskirti gamintojui, kuris projektuoja gaminį, o ne vartotojui. Jas reikia įvertinti ir panaudoti sprendžiant gamybos optimizavimo uždavinį.

Asimetrijų optimumai, nominalas, konstruktyvinės paklaidos

Turint optimizuotas asimetrijų normas, toliau galima spręsti konstruktyvinių paklaidų arba asimetrijų nominalo (tikslo) optimizavimo klausimą. Šitam darbui pasitelkiam aukščiau minėtus asimetrijų sluoksnius, suformuotus koreliacinės analizės metu, atskirai eilučių ir kadrų ritelėms. Tokiu būdu gaunasi aštuoni asimetrijų sluoksniai kuriuose, įskaitant ir astigmatizmo bei komos tarpines kineskopo zonas bei po vieną skleistinės geometrijos asimetriją, yra po vienuolika asimetrijų. Turint pakankamą kiekį matavimų, galima projektuoti tinkamumo ar defektingumo grafikus kiekvienai asimetrijai ir paskaičiuoti bendrą tinkamumą ar defektingumą kiekvienam sluoksniui, kuriame atsispindės to sluoksnio asimetrijų optimumas, kuris privalo tapti gamybinio proceso tikslu ar nominalu, atspindėti konstruktyvines paklaidas.

Kritiniai asimetrijų parametrai ir gamybiniai objektai.

Kiekvieno sluoksnio bendro tinkamumo arba defektingumo grafikas suformuojamas įvertinant kitų to sluoksnio asimetrijų parametrus ir turi optimumo zoną. Arčiausiai šio grafiko esantys asimetrijų grafikai daro didžiausią įtaką jam ir yra priskiriami kritinėms asimetrijoms, kuriems reikia skirti didesnį dėmesį, koreguoti technologinį procesą ar asimetrijų normas ir t.t. O kadangi optimumus galima skaičiuoti ir atskirai kiekvienam objektui, tai analogiškai galima rasti ir kritinius gamybinius objektus, kurie gadina bendrą tinkamumo vaizdą. Toliau kiekvienam objektui atskirai vėl galima skaičiuoti optimumus ir rasti kritines asimetrijas. Tokiu būdu gamybos proceso inžinierius gauna patikimą gamybos proceso valdymo įrankį. Atlikus technologinio proceso koregavimą, minėtomis procedūromis galima tikėtis žymaus kokybės pagerėjimo ir gamybinių nuostolių sumažėjimo.

Gaminys	Eilučių rit. kritinės asimetrijos				Kadrų rit. kritinės asimetrijos
Gaminys	M	D	N	W	M	D	N	W
1	S0AP02 S3AP17	S0AP20	S0AP06 GP30	S0AP08	S0AP01 S0KP09	S3AP03	S0AP05	-
2	S0AP02 S3AP17	S0AP20	S0AP06 S0AP14	S0AP08 S3AP16	S0AP01 S0KP09	S0AP03 S0AP19	S0AP05 S0AP13	GP31
3	S0AP02 S0AP17	-	GP30 S0AP06	S0AP08	S0AP01 S0KP01	-	S0AP05	S0AP07
4	S0AP02 S0AP17	-	-	S0AP08	S0AP18	-	S0AP05 S0AP13	S0AP07 S0AP15

4 lentelė. Įvairių gaminių kritiniai asimetrijų parametrai

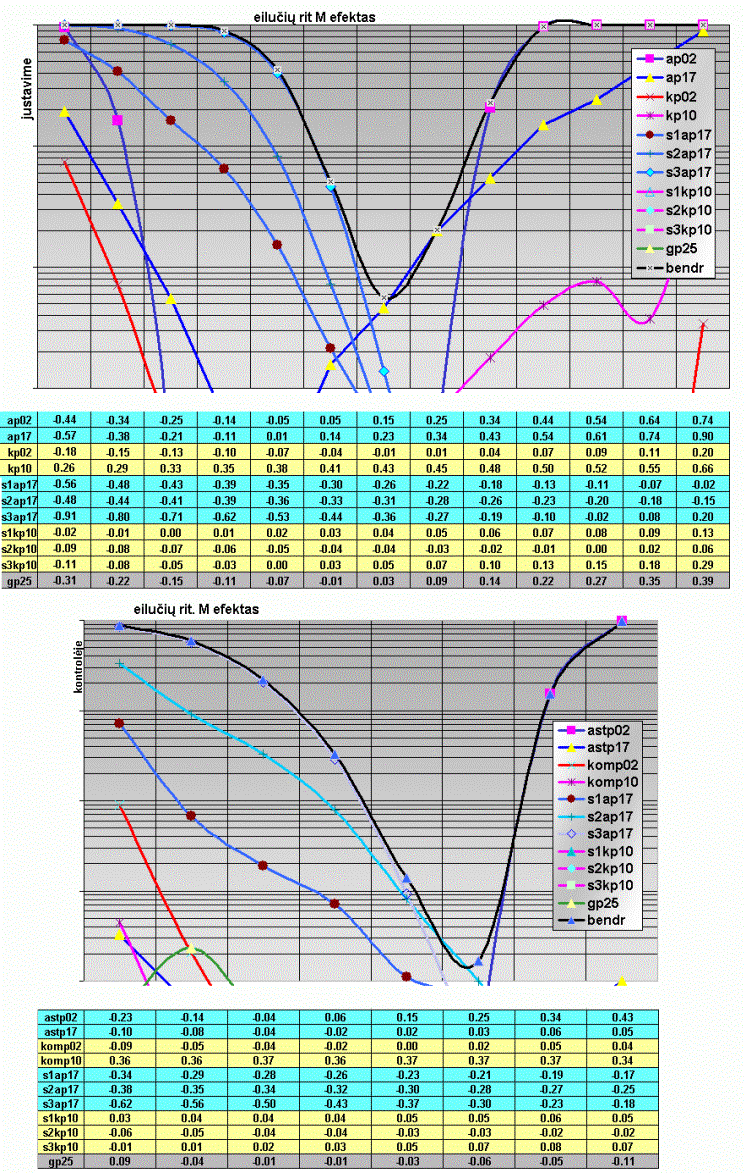
Pieš. 6. Optimalių asimetrijų formavimo grafikų pavyzdžiai

Šioje lentelėje S0, S1, S2, S3 žyminiais pažymėtos asimetrijos parametrų zonos kineskopo ekrane. Toliau AP-astigmatizmo, KP-komos ir GP-geometrijos asimetrijų parametrai. Žyminio gale nurodytas asimetrijos parametro numeris aukščiau esančioje asimetrijų lentelėje.

Ne mažiau įdomus ir kritinių gamybinio proceso objektų sąrašas, gaunamas nagrinėjant jų skirtumus grafiniame lauke. Tai objektai, išsiskiriantys blogesnėmis derinimo galimybėmis. Turint šiuos grafikus galima identifikuoti, taisyti ir koreguoti ne tik parametrus bet ir gamybinio proceso objektus - stakles, įrankius, matavimo priemones.

Gaminys

Eilučių rit. kritiniai gamybos obj.

Kadrų rit. kritiniai gamybos obj.

Enr2;3

Enr6

Enr5;7;11;13;

Kin21

Enr6

Knr401;404;

Kin70

6 lentelė. Gaminio kritiniai gamybinių objektų žyminiai

Šioje lentelėje Enr – eilučių įspraustinės Nr.; Knr – kadrų staklių laikiklis; Kin – kontrolės įrenginio kineskopas;...

Galima padaryti ir geriausių objektų sąrašą, kuriuos panaudoti kaip pavyzdžius ar etalonus. Atskira gamybinių objektų rūšis – registruojami kompiuterinėse duomenų bazėse darbuotojai, gamybinių operacijų atlikėjai. Aiškiai matosi, kad vieniems gaunasi geriau, kitiems blogiau.

Eilučių ir kadrų ritelių asimetrijų optimumai

Jei panagrinėsime atskirai eilučių ir kadrų, atskirai kiekvieno efekto asimetrijos parametrų optimumų grafikus, pamatysime aiškiai ir nepakankamai išreikštus optimumus.

Gaminys	Eilučių rit. optimumų galimybės				Kadrų rit. optimumų galimybės
Gaminys	M	D	N	W	M	D	N	W
1	-0,05 0 5	~ 0,2 0			0,0 0 4	0,0 0,48 0
2	0,0 0 2	~ +0,08 ~ 0,36 0	~ -0,24 ~ 0,13 0,1	+0,13 0 8	0,0 0 9	-0,05 0,42 0	-0,05 0,2 0,3	neaiškus 0,1 0,3
3	0.0 0,39 0	nėra	~ -0.2 0,20 0,1	-0.1 0,40 0	0.0 0,32 0	nėra	0.0 0,40 0	0,0 0,32 0
4	-0,17 0,45 0	nėra	nėra	-0,1 0,20 0,2	~ +0,17 ~0,26 0,02	nėra	+0,1 0,49 0	+0,05 0,25 0,105

7 lentelė. Įvairių gaminių optimumų realizacijos galimybių įvertinimas

Šioje lentelėje pirmas iš viršaus skaičius rodo optimumo poslinkį nuo vidurkio matuojant asimetriją ant ašies, antras skaičius – optimumo plotį nustatytame lygyje ir trečias – bendro optimumo minimumą. Skaitinės šios lentelės reikšmės reikalauja nagrinėjimo ir patikslinimo, nes gautos atliekant pirmą bandomąjį skaičiavimą. Trečiam ir ketvirtam gaminiui nebuvo tarpinių zonų duomenų.

Daug įdomių išvadų galima daryti minėta kompiuterine programa analizuojant įvairiais pjūviais įvairius asimetrijų sluoksnius. Įdomus eilučių ritelių D efektas. Jis parodo, kad visas vyniojimo įspraustines reikia koreguoti ir tobulinti gamybos technologiją. Labai žymią įtaką technologinio proceso parametrams daro matavimams skirtų kineskopų keitimai ir N efekto pokyčiai. Jų parametrams reikia skirti daugiau dėmesio. Dar ši programa leidžia tikrinti skirtingų gamybinių objektų suderinamumą, filtruojant duomenis ir analizuojant tik vieno objekto duomenis ir kokie gaunasi optimumai su kitais objektais. Tokiu būdu galima patikrinti objektų suderinamumą. Gal kokios tai eilučių staklės daugiau derinasi su kokiom tai konkrečiom kadrų ritelių staklėm ar kita įranga.

Pasikliautini intervalai

Aukščiau pateiktose lentelėse panaudoti gamybinio proceso matavimų duomenų apimtys nuo pusės iki metų laikotarpio. Matavimų skaičius priklausomai nuo gaminio - nuo 6000 iki 200000. Tokiai didelei imčiai tinkamumo ir defektingumo pasikliautini intervalai yra pakankamai maži ir gautų rezultatų patikimumas pakankamai didelis. Pavyzdžiui tinkamumo rodikliui Cpk pasikliautini intervalai skaičiuojami remiantis sekančia formule:

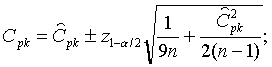
Kai n=6000, gaunasi sekančios reikšmės: Cpk=1,00±0,02.

Išvados

KS gamybinio proceso asimetrijų normas bei konstruktyvines paklaidas ar gamybos tikslus tikslinga išnagrinėti ir optimizuoti aukščiau nurodytu metodu. Šiam tikslui sukurti ir panaudoti kompiuterines programas, kurios panaudoja esančius matavimų duomenis bei įvertina esantį parametrų pasiskirstymą.

Įtraukti į KS gamybos technologinį procesą ir apmokyti darbuotojus naudotis naujomis kompiuterinėmis programomis ir asimetrijų sumos dėsniais. Išnaudoti asimetrijos parametrų Mr4, Md4, Dr4, Dd4, Nr6,Nd6, Wr6, Wd6 galimybes. Dokumentacijoje nurodyti būtiną optimumų paskaičiavimą kas ketvirtį ir po žymių technologijos proceso pakeitimų. Įtraukti į duomenų bazę technologinio proceso ir įrangos pakeitimų formas ir lenteles. Didesnį dėmesį skirti kineskopų pakeitimams ir parametrų koregavimui bei jų registravimui kompiuterinėse rinkmenose. Išbandyti eilučių ritelių įspraustinių koregavimą, remiantis D efekto optimumais. Išanalizuoti metodo pritaikymo galimybes kineskopų gamyboje.

Kreipiamųjų sistemų parametrų statistinė analizė

Vytautas Šaras (AB “Vilniaus Vingis”)

Pranas Vaitkus (VU Matematinės statistikos katedra)

Kam reikalingi proceso atitikmens indeksai. Palyginimas su defektingumu.

Statistinėje procesų valdymo teorijoje atskirai naudojamos vidurkių poslinkio kontrolės kortos(), proceso parametro išsibarstymo kontrolės kortos (R, S). Normalaus dėsnio atveju vidurkio įvertis ir dispersijos įvertis S yra nepriklausomi dydžiai. Todėl ir reikalingos dvi kontrolės kortos. Kad surišti vienu dydžiu specifikacijos normas su parametro išsibarstymo dydžiu buvo pasiūlytas proceso atitikmens indeksas , kur USL ir LSL- viršutinė ir apatinė specifikacijos linijos, - parametro standartinis kvadratinis nuokrypis. Taguchi ir kt. 1985 m. pasiūlė jautresnį indeksą C. Skaitoma, kad procesas geras, jei arba

Iš čia matome, kad reikšmė apibūdina intervalą, į kurį turi patekti parametro vidurkio įvertis:

LSL+4

Kadangi įverčiai yra atsitiktiniai dydžiai, tai turime kalbėti apie tolesni įvykių tikimybes:

kur yra defektingumo lygis. Antra vertus, jei žinome, kad , tai gauname, kad

kai L=a-4, V.

Taigi, jei nenorime keisti proceso ir kontrolės ribų a ir b, tai turime laikyti, kad specifikacijos linijos yra a-4, .

Jei fiksuotas lygmuo 1- ir USL=-LSL, tai USL randame iš sąlygos

Proceso atitikmens rodiklių variantai.

Minėti atitikmens indeksai ir turi savų trūkumų, nes neatsižvelgia į tai kaip skiriasi proceso vidurkis nuo jo optimalios, iš anksto nusakytos padėties T. Todėl buvo pasiūlytas indeksas

ir jo apibendrinimas , kur

d=(USL-LSL)/2, m=(USL+LSL)/2. Aišku, kad , kai , , kai , , kai . Reikia pabrėžti, kad šie indeksai naudojami ir jų parametrai vertinami kai procesas yra kontrolės būsenoje ir parametras pasiskirstęs pagal normalųjį dėsnį . Be to dažniausiai imamos simetrinės specifikacijos linijos

-LSV= USL=SL. Tada m=0, d=SL. Jei normališkumo hipotezė atmetama, tai galima naudoti suglodintus adaptyvius indeksų ir įverčius

kur , SA=- svertinis matavimų variacinės eilutės vidurkis, , yra [] mažiausių ir didžiausių variacinės eilutės vidurkių skirtumas.

Proceso atitikmens indeksai negali apibūdinti visas praktikoje pasitaikančias situacijas. Todėl vietoje to, kad nagrinėti intervalų, aibių matų santykį, M. Perakis ir E. Xekalakis (2003) pasiūlė nagrinėti proceso tinkamumo tikimybių santykį, kurio pagalba nusakomas atitikmens indeksas . Čia yra iš anksto duotas, susitartas, proceso mažiausiai leistinas tinkamumo procentas (tikimybė).

Intuityviai aišku, kad turi būti artimas vidurkiui, pvz . Tada

Vienintelis nežinomas dydis yra tikimybė p, kurią reikia įvertinti pagal turimus stebėjimo duomenis ir pagal prielaidas apie procesą charakterizuojančio parametro tikimybinį pasiskirstymą. Paprasčiausiu, normalaus dėsnio atveju, turime

Paėmę parametrų ir įverčius ir S Gauname tikimybės p įvertį

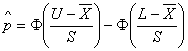Šis įvertis yra atsitiktinis dydis ir yra pastumtas įvertis. Todėl į formulę reikia įstatyti apatinę 100(1-)% pasikliovimo lygio įverčio ribą :

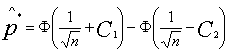, kur

Tuo pačiu galima teigti, kad , t. y. yra apatinė riba atitikmens indeksui . Skaitysime, kad procesas atitinka specifinius reikalavimus, jei .

Proceso atitikmens rodiklio tikimybiniai intervalai.

Shiau ir kt. (1999) pasiūlė konstruoti pasikliautinuosius intervalus atitikmens indeksų kvadratams. Jų rezultatai yra tokie

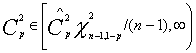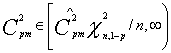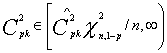
su tikimybe 1-p.

Pasikliautinieji intervalai svarbus, kai reikia nustatyti parametro matavimų imties tūrį. L. R. A. Franklin (1999) pateikė formules, kaip rasti n, kai žinomas santykis =A, kur yra (1-)100% apatinė pasikliautinoji riba. Imdami, pavyzdžiui, ir A=0.08 gauname n=36. Panašios formulės pateiktos ir rodikliams bei . Kelių autorių darbuose yra pateiktos indekso įverčio pasiskirstymo funkcijos išraiškos, kurias galima panaudoto konstruojant pasikliautinuosius intervalus.

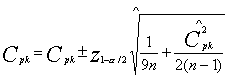
KS gamybos proceso įvertinimo apibendrinantis rodiklis.

Anksčiau buvo nagrinėjama situacija, kai procesas charakterizuojamas vienu parametru (vienmatis atvejis). Tačiau KS atitikimas specifikacijos normoms nusakomas daugeliu parametrų (daugiamatis atvejis). Taamas ir kt. (1993) pasiūlė tokį daugiamatį atitikmens rodiklį

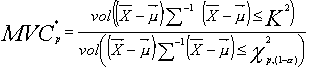kur parenkamas taip, kad elipsoidas , kurio tūris yra rodiklio skaitiklyje, būtų specifikacijos srities viduje. Čia , , yra vektoriaus koreliacinė matrica, paprastai lygus 0.0027, yra dėsnio kvantilis. Jessenbergas ir kt. parodė, kad

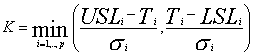Nickersonas (1994) pasiūlė patalpinti elipsoidą

į mažiausio tūrio stačiakampį gretasienį su ribomis

Tada galima apibrėžti tokį atitikmens indeksą

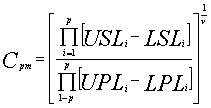Chanas (1994) pasiūlė naudoti atitikmens indeksą , kai tolerancijos zona V yra nusakoma taip:

Čia gali būti bet kokia techninių sąlygų nusakyta funkcija. Skaitome, kad procesas tinkamas, jei , kur yra leistinas defektingumo lygis. Randame r tokį, kad

Tada procesas tinkamas, jei , tai yra . Todėl daugiamatis atitikmens indeksas nusakomas taip . Jei tolerancijos zona V yra stačiakampis gretasienis

tai atitikmens indeksas bus , kur r tenkina sąryšį

Jei r<1,tai ir procesas yra tinkamas. Praktikoje galima elgtis taip. Sudarome stebėjimų imtį ir ieškome mažiausio r, kad

Jei rastas r<1, tai procesas patenka į tolerancijos zoną, jei r>1, tai reikia ieškoti defekto priežasčių.

Neuroninių tinklų taikymo variantų pasirinkimo klausimu.

Neuroninių tinklų pagalba sprendžiami klasifikavimo, klasterizavimo, regresijos, atpažinimo, valdymo uždaviniai. Sukurta daug jų apmokymo algoritmų, kai iš anksto pasirenkama neuroninio tinklo architektūra. Čia paliesime tik sąlyginių tikimybių modeliavimą neuroninių tinklų pagalba.

Tarkime, technologinio proceso būseną nusako parametras Y, kuris yra funkcija nuo stebimų, matuojamų parametrų vektoriaus , t. y. . Kadangi funkcija f paprastai nežinoma, tai galima spręsti regresijos uždavinį: rasti neuroninį tinklą tokį, kad su tam tikru patikimumu. Galima formuluoti ir kitą uždavinį: rasti aprašantį tikimybes . Šiuo atveju galima imti tokią neuroninio tinklo struktūrą

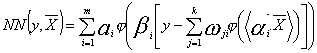kur , , – sigmoidinė funkcija. Panaudojus maksimalaus tikėtinumo principą ir globalaus ekstremumo taško radimo algoritmą, reikia rasti parametrų įverčius, kai turime apmokymo aibę . Apmokius neuroninį tinklą gauname ir sąlyginių vidurkių bei dispersijų aproksimacijas:

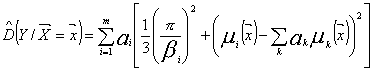kur

Šias aproksimacijas galima panaudoti sąlyginių kontrolės kortų konstravime. Tarkime, technologinis procesas laikomas geru, jei , t. y. Y patenka į specifikacijos intervalą. Tada tikriname ar . Šių nelygybių pagalba mes nusakome sritį V tokią, kad jei , tai procesas yra geras.